- 6.4 Properties Of Definite Integralsap Calculus Solver
- 6.4 Properties Of Definite Integralsap Calculus Algebra
- 6.4 Properties Of Definite Integralsap Calculus Calculator
Using Properties of Definite Integrals Some quick examples of how the properties of definite integrals can be used to calculate integrals of unknown functions. FUN-6.A.2 Properties of definite integrals include the integral of a constant times a function, the integral of the sum of two functions, reversal of limits of integration, and the integral of a function over adjacent intervals. FUN-6.A.3 The definition of the definite integral may be extended to functions with removable or jump discontinuities. 4.4 Properties of Definite Integral 132 4.5 Trapezoidal Rule 135 4.6 The Fundamental Theorem of Calculus Part 1 139.


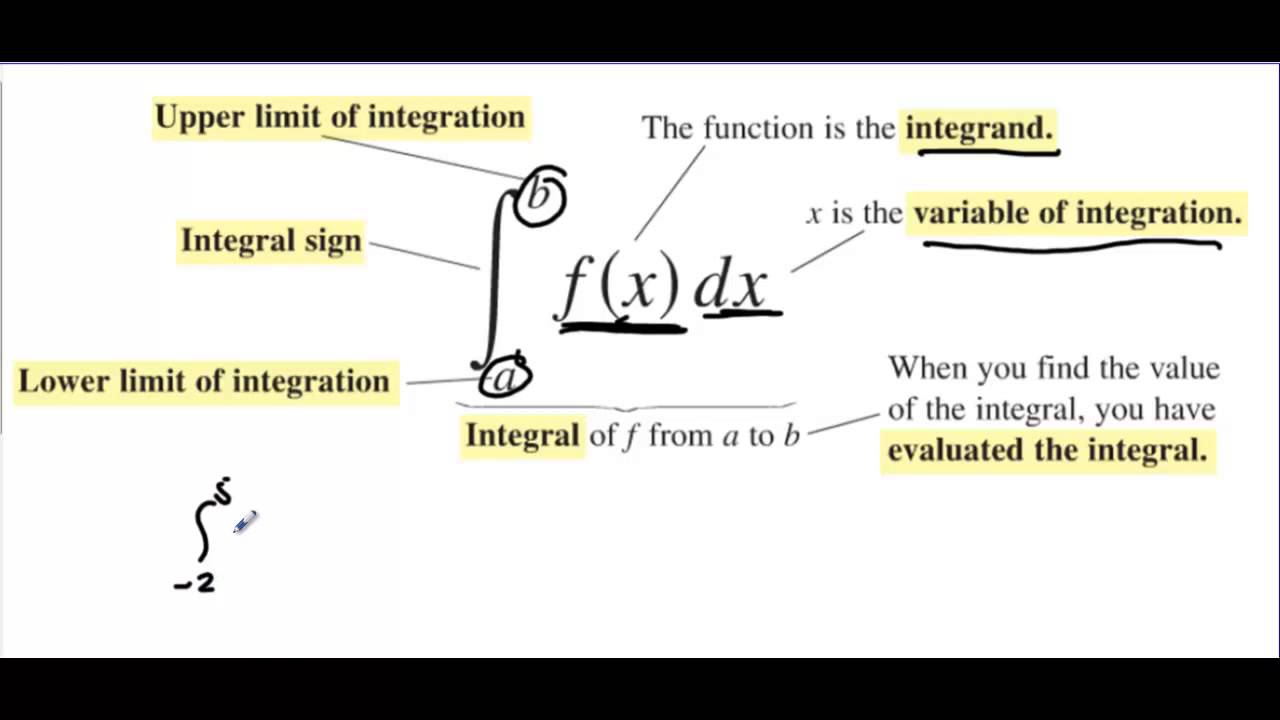
Antiderivatives: (F), (G)
Independent variables: (x), (t)
Limits of integration: (a), (b), (c), (d)
Answer: A definite integral refers to an integral with upper and lower limits. If it is restricted to exist on the real line, the definite integral is called by the name of Riemann integral. Question 3: Differentiate between indefinite and definite integral? Answer: A definite integral is characterized by upper and lower limits. 6.1: Substitution This chapter is devoted to exploring techniques of antidifferentiation. While not every function has an antiderivative in terms of elementary functions (a concept introduced in the section on Numerical Integration), we can still find antiderivatives of a wide variety of functions.
6.4 Properties Of Definite Integralsap Calculus Solver

6.4 Properties Of Definite Integralsap Calculus Algebra
Arbitrary point of a subinterval: ({xi_i})
Natural numbers: (n), (i)
Area of a curvilinear trapezoid: (S)
6.4 Properties Of Definite Integralsap Calculus Calculator
- Let a real function (fleft( x right)) be defined and bounded on the interval (left[ {a,b} right]). Let us divide this interval into (n) subintervals. In each interval, we choose an arbitrary point ({xi_i}) and form the integral sum (sumlimits_{i = 1}^n {fleft( {{xi _i}} right)Delta {x_i}}) where (Delta {x_i}) is the length of the (i)th interval. The definite integral of the function (fleft( x right)) over the interval (left[ {a,b} right]) is defined as the limit of the integral sum (Riemann sums) as the maximum length of the subintervals approaches zero.
(require{AMSmath.js}{largeintlimits_a^bnormalsize} {fleft( x right)dx} =) (limlimits_{substack{n to inftytext{max},Delta {x_i} to 0}} sumlimits_{i = 1}^n {fleft( {{xi _i}} right)Delta {x_i}} ,) where (Delta {x_i} = {x_i} – {x_{i – 1}},) ({x_{i – 1}} le {xi _i} le {x_i}.) - The definite integral of (1) is equal to the length of the interval of integration:
({largeintlimits_a^bnormalsize} {1,dx} = b – a) - A constant factor can be moved across the integral sign:
({largeintlimits_a^bnormalsize} {kfleft( x right)dx} =) ( k{largeintlimits_a^bnormalsize} {fleft( x right)dx} ) - The definite integral of the sum of two functions is equal to the sum of the integrals of these functions:
({largeintlimits_a^bnormalsize} {left[ {fleft( x right) + gleft( x right)} right]dx} =) ( {largeintlimits_a^bnormalsize} {fleft( x right)dx} + {largeintlimits_a^bnormalsize} {gleft( x right)dx} ) - The definite integral of the difference of two functions is equal to the difference of the integrals of these functions:
({largeintlimits_a^bnormalsize} {left[ {fleft( x right) – gleft( x right)} right]dx} =) ( {largeintlimits_a^bnormalsize} {fleft( x right)dx} – {largeintlimits_a^bnormalsize} {gleft( x right)dx} ) - If the upper and lower limits of a definite integral are the same, the integral is zero:
({largeintlimits_a^anormalsize} {fleft( x right)dx} = 0) - Reversing the limits of integration changes the sign of the definite integral:
({largeintlimits_a^bnormalsize} {fleft( x right)dx} =) ( -{largeintlimits_b^anormalsize} {fleft( x right)dx}) - Suppose that a point (c) belongs to the interval (left[ {a,b} right]). Then the definite integral of a function (fleft( x right)) over the interval (left[ {a,b} right]) is equal to the sum of the integrals over the intervals (left[ {a,c} right]) and (left[ {c,b} right]:)
({largeintlimits_a^bnormalsize} {fleft( x right)dx} =) ( {largeintlimits_a^cnormalsize} {fleft( x right)dx} ) (+; {largeintlimits_c^bnormalsize} {fleft( x right)dx}) - The definite integral of a non-negative function is always greater than or equal to zero:
({largeintlimits_a^bnormalsize} {fleft( x right)dx} ge 0) if (fleft( x right) ge 0 text{ in }left[ {a,b} right].) - The definite integral of a non-positive function is always less than or equal to zero:
({largeintlimits_a^bnormalsize} {fleft( x right)dx} le 0) if (fleft( x right) le 0 text{ in } left[ {a,b} right].) - Fundamental theorem of calculus
({largeintlimits_a^bnormalsize} {fleft( x right)dx} =) ( {left. {Fleft( x right)} right|_a^b} =) ( Fleft( b right) – Fleft( a right),) if (F’left( x right) = fleft( x right).) - Substitution rule for definite integrals
If (x = gleft( t right)), then ({largeintlimits_a^bnormalsize} {fleft( x right)dx} =) ({largeintlimits_c^dnormalsize} {fleft( {gleft( t right)} right)g’left( t right)dt}, ) where (c = {g^{ – 1}}left( a right),) (d = {g^{ – 1}}left( b right).) - Integration by parts for definite integrals
({largeintlimits_a^bnormalsize} {udv} =) (left.{left( {uv} right)}right|_a^b – {largeintlimits_a^bnormalsize} {vdu} ) - Trapezoidal approximation of a definite integral
({largeintlimits_a^bnormalsize} {fleft( x right)dx} =) (largefrac{{b – a}}{{2n}}normalsizeBig[ {fleft( {{x_0}} right) + fleft( {{x_n}} right) }) (+;{ 2sumlimits_{i = 1}^{n – 1} {fleft( {{x_i}} right)} } Big]) - Approximation of a definite integral using Simpson’s rule
({largeintlimits_a^bnormalsize} {fleft( x right)dx} =) ({largefrac{{b – a}}{{3n}}normalsize}Big[ {fleft( {{x_0}} right) + 4fleft( {{x_1}} right) }) (+;{2fleft( {{x_2}} right)}) (+;{ 4fleft( {{x_3}} right) + 2fleft( {{x_4}} right) + ldots}) (+;{4fleft( {{x_{n – 1}}} right) + fleft( {{x_n}} right)} Big],)
where ({x_i} = a + {largefrac{{b – a}}{n}normalsize} i,) (i = 0,1,2, ldots ,n.) - Area under a curve
(S = {largeintlimits_a^bnormalsize} {fleft( x right)dx} =) (Fleft( b right) – Fleft( a right),) where (F^{,prime}left( x right) = fleft( x right).) - Area between two curves
(S = {largeintlimits_a^bnormalsize} {left[ {fleft( x right) – gleft( x right)} right]dx} =) (Fleft( b right) – Gleft( b right) ) (-;Fleft( a right) + Gleft( a right),) where (F^{,prime}left( x right) = fleft( x right)), (G^{,prime}left( x right) = gleft( x right).)
